Bipartite Graphs
Algorithmically Speaking - #14: The basic definitions of bipartite graphs, some context in which they are used, and some example problems where we can find them.
Hello there!
Welcome to Algorithmically Speaking, where we discuss topics on the intersection of Computer Science, Software Engineering, and life.
This post is taken directly from my upcoming book, The Competitive Programmer Graphs Handbook, a graph theory book focusing on three main topics: bipartite graphs, functional graphs, and Euler paths. You can read all the details here:
You can play a crucial role in bringing this book to life by preordering your digital, DRM-free copy. By doing so, you'll receive early and frequent updates, including all future editions.
This chapter is a comprehensive guide to identifying and solving graph theory problems involving bipartite graphs. It will equip you with the necessary theoretical background and practical techniques to tackle such tasks.
As will be the case throughout the book, the chapter begins with a section dedicated to defining all the theoretical background related to the topic to be discussed, which is necessary for solving the problems that will be presented later. Then, the intention is to show the most common techniques and ideas used when facing tasks of this type through the resolution of several algorithmic problems.
Before we begin, if you think you need a refresher on the basics of graph theory to take the most out of today’s discussion, please look at the previous articles of this series:
Let’s get started!
Basic Definitions
An undirected graph G is called bipartite when it is possible to partition the set V of its vertices into two sets, A and B, such that for every edge, one end belongs to A and the other to B. More colloquially, it is often interpreted as the vertices assigned to set A being colored blue and those assigned to set B being colored red. Thus, in this way, a graph can be considered bipartite if it is possible to color its vertices with two colors, such that the ends of each edge have different colors.
Thinking about what types of graphs are not bipartite can give an idea of some necessary conditions for the above property to hold. For example, if there is a triangle and one vertex is colored red and another blue, any color assigned to the remaining vertex will conflict with one of its two neighbors.
In general, if an odd-length cycle exists with the vertices numbered 1, 2, …, 2k, 2k + 1. Assuming that the odd vertices are colored red and the even ones are blue up to vertex 2k when it comes time to assign a color to vertex 2k + 1, no color assigned to it will be valid because it shares an edge with a blue-colored vertex and another with a red-colored one.
The following proposition derives from this fact:
Proposition 1. If an undirected graph G is bipartite, it contains no odd-length cycles.
Graph Classification
Recognizing if a graph is bipartite when the sets A and B are defined beforehand is relatively simple. If the sets are well chosen, there will be no edge with both ends belonging to the same set. Therefore, to check if the bipartition (A, B) is valid, it is sufficient to iterate through the edges, verifying that both ends belong to different sets.
However, given an arbitrary undirected graph, the task of determining if it is bipartite or not becomes more complex. An algorithm will be presented below to check this condition in graphs and demonstrate that odd-length cycles are the only impediment to a graph being bipartite.
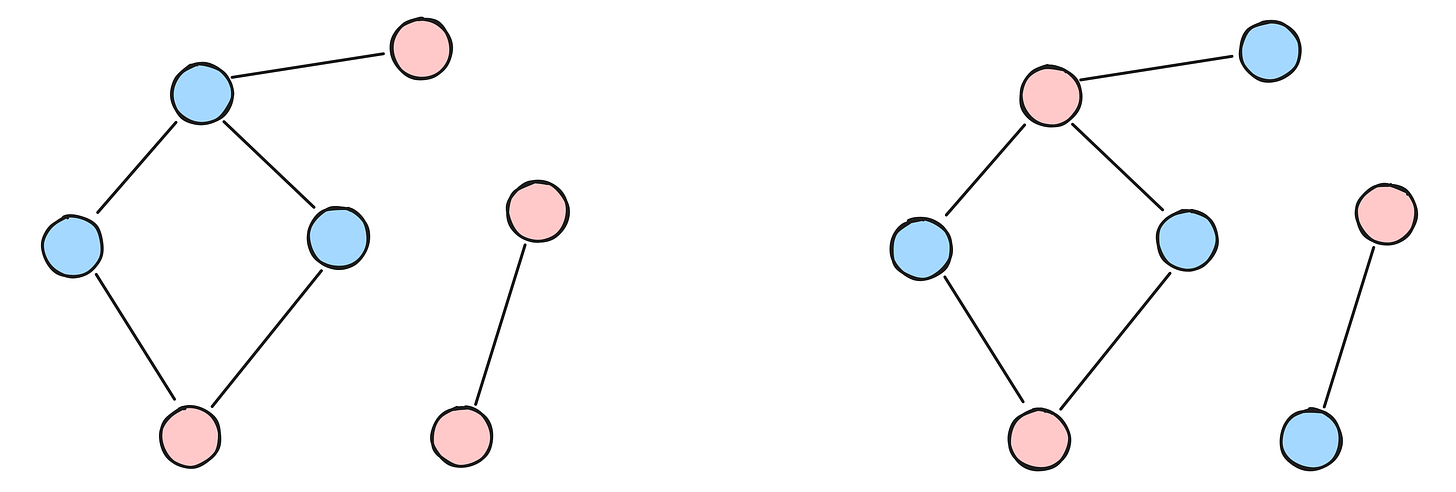
First, graph G will be assumed to be connected. If not, each connected component must be checked independently to determine whether it is bipartite.
The algorithm starts by selecting a vertex that belongs to V and assigning it a color. The assigned color does not matter since it must receive some color anyway, so it will be assumed that red is assigned. The neighbors of this vertex must be colored blue, and in turn, the neighbors of these will be assigned the color red. This continues until no vertices are left uncolored.
At this point, either a valid coloring of the graph is achieved, or there is an edge with both ends of the same color. If the latter occurs, there is nothing the algorithm could have done to change the result; the graph is not bipartite.
The algorithm described above is essentially the description of BFS: starting from an origin, a vertex is colored the first time it is discovered. One way to describe the graph coloring process is to interpret the BFS algorithm as follows: vertices in odd layers are colored red, and those in even layers are colored blue.
Modifying the BFS algorithm presented before is straightforward if one wants to determine if a graph is bipartite; add an array color[u] that indicates the color assigned to vertex u. When a vertex v is to be added to its layer, color[u] is assigned the value red or blue depending on the parity of the layer it belongs to.
Proposition 2. Let G be a connected undirected graph and C1, C2, … the layers produced by the BFS algorithm starting at a vertex s. Then exactly one of these two things can occur:
There is no edge connecting two vertices that belong to the same layer. In this case, G is bipartite since the vertices in even layers are colored one color, and those in odd layers are colored the opposite color.
An edge connects two vertices belonging to the same layer. In this case, G contains an odd-length cycle and, therefore, cannot be bipartite.
Proof. Consider the first case, where it is assumed that there is no edge connecting vertices of the same layer. According to the BFS algorithm, each edge of G connects vertices belonging to the same or adjacent layers. In this case, only the second option can occur. The proposed coloring assigns different colors to layers of different parity; therefore, each edge will have endpoints with different assigned colors. This implies that the graph is bipartite.
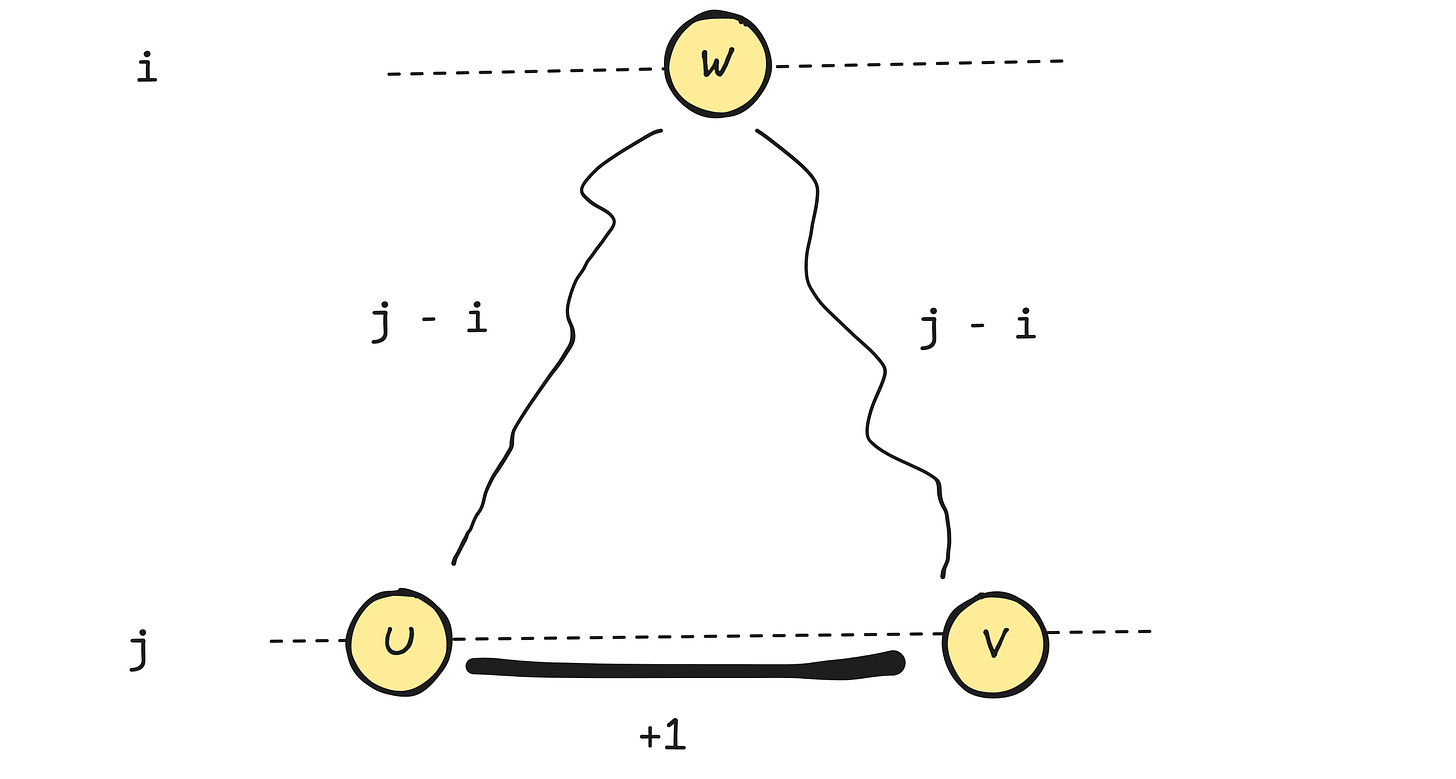
Considering the second case, the question is why this graph must have an odd-length cycle. It is known that there is an edge where both ends belong to the same layer. Let this edge be e = (u, v), with u, v ∈ Cj. Considering the BFS tree generated by the BFS algorithm, let w be the vertex whose layer is the highest possible and is an ancestor of both u and v in this tree. This vertex is the lowest common ancestor of u and v. Assuming that w ∈ Ci with i < j, there is a cycle in the graph consisting of the paths from w to u, w to v, and the edge (u, v). The length of this cycle is (j − i) + (j − i) + 1. Grouping similar terms, we get 2 · (j − i) + 1, so the length of this cycle is odd. ∎
Context
When discussing bipartite graphs, there are not many elements to consider. Beyond that they can be viewed as equivalent to a bicoloring of the graph and do not have odd-length cycles, they do not present many more relevant details. However, problems related to bipartite graph theory are often interesting because of the ways in which the few properties these graphs have can be applied to solve complex tasks.
One of the most challenging tasks is properly recognizing when a problem is related to bipartite graphs. This requires noticing a series of recurring patterns that appear in such tasks.
For example, when some constraint involves splitting elements into two sets, the problem is likely related to bipartite graphs. Coloring problems are a classic example of this. Even if the problem involves more than two sets, it is advisable to take some time to analyze whether or not there is some kind of equivalence between these sets so that it can be reduced to working with two sets.
There are situations where reducing to bipartite graphs greatly simplifies the solution. Take, for example, problems related to matchings. In general graphs, finding a maximum matching has a computational cost of O(|V|^4) using the Blossom algorithm. However, the same problem in bipartite graphs can be solved in O(√|V| · |E|) using the Hopcroft-Karp algorithm.
Thinking in terms of bipartite graphs does not always indicate that a specific algorithm for these graphs must be used to solve a particular problem. It can also be useful to highlight some properties that, overlooking the fact that the graph is bipartite, might go unnoticed. As an example of this, consider the following problem:
Problem 1. There are n segments located on the number line. Each segment is assigned one of two colors: red or blue. The goal is to find a subset of these segments of maximum cardinality such that no two segments of different colors in this set intersect.
This problem has several solutions using dynamic programming techniques that rely on data structures for querying and updating information over ranges. Such solutions generally require attention to many implementation details and usually consume a lot of time, especially if one is unfamiliar with using advanced data structures or the fundamentals of dynamic programming.
However, the following interpretation of the problem allows for a much simpler solution:
Each segment corresponds to a vertex in an undirected graph G, and if the corresponding segments intersect and are of different colors, there is an edge between vertices u and v. Therefore, this can be interpreted as a bipartite graph in which the colors of the segments determine the sets A and B.
Framed in this way, the problem reduces to finding an independent set of maximum cardinality in G, which is easy to solve using the maximum matching algorithm for bipartite graphs (see Kőnig's theorem). Even better, the geometric structure of the problem allows for a simple greedy algorithm to be implemented to obtain this maximum independent set.
If you know the greedy algorithm to solve this problem, leave a comment below.
In the previous example, the key to a simple solution was noticing that we were dealing with a bipartite graph.
Another recurrent example of a bipartite graph is bi-dimensional arrays. Problems posed on a two-dimensional matrix are often related to graph theory. Moreover, the following observation allows, in some cases, to think about bipartite graphs in this context:
If the matrix is colored like a chessboard, the positions (i, j) where i + j is even are assigned the same color and those where i + j is odd are assigned the opposite color.
The above fact is often useful when the problem involves maybe some kind of game in which your character needs to traverse this matrix. If it is defined that from a cell (i, j), one can move up, down, left, or right, then each position in the matrix can be interpreted as a vertex of an undirected graph. Each node has edges with at most four vertices corresponding to its adjacent positions. The resulting graph is bipartite since two adjacent cells receive different colors in the chessboard-like coloring.
Finally, it is known that the presence of odd-length cycles is the only impediment for a graph to be bipartite. Therefore, acyclic graphs are bipartite.
This fact can be helpful when dealing with a problem related to trees. Trees often appear in problems involving DFS or BFS traversals, dynamic programming, or advanced data structures such as segment trees. However, in some cases, the key piece of information to solve the problem is that trees are also a bipartite graph.
As it has been shown, bipartite graphs often appear implicitly in numerous contexts, and therefore, recognizing them can be challenging. Moreover, the large number of types of tasks involving them makes solving the problem, once the bipartite graph is identified, highly complex in terms of reasoning and implementation.
The next edition related to bipartite graphs will start covering sample problems so we can start experiencing the thinking process and solution implementation of these types of tasks hands-on.
Stay tuned.
And that’s it for today! If you are finding this newsletter valuable, consider doing any of these:
1) ✉️ Subscribe to the newsletter — if you aren’t already, consider becoming a free or paid subscriber.
2) 💛 Get early access to my book— thanks to all of you who have contributed to support my writing. The book I'm writing covers this and similar topics in more depth.
3) 🍻 Read with your friends — this newsletter grows because readers share. I don’t use social media too much to advertise my writing. I’m counting on you!
Have a great day! ☀️
Alberto












This has been my favourite post so far, and I’m eager to read more like it. Very nicely introduced and described
Nice post, very instructive I'm implementing this algorithm rn, please bring this kind of topics more often